Iniciaremos con la definición de sucesiones, su clasificación con relación a la operación que genera sus términos y que se muestra en los siguientes videos del Canal de You Tube MATH2Me :
SUCESIONES ARITMÉTICAS
- Completar la sucesión 9,20,29,36,41...
- Obtener el término enésimo y los términos a partir de la función de la sucesión
Suma de n términos de la sucesión
SUCESIONES GEOMÉTRICAS
Obtener la función de una progresión geométrica
Obtener la suma de una progresión geométrica
Obtener la función y Suma de una progresión geométrica a partir del valor de n términos
PROBLEMAS DE APLICACIÓN DE PROGRESIONES GEOMÉTRICAS
SUCESIONES: ALFANUMÉRICAS, SIMBÓLICAS Y GRÁFICAS
A veces los números forman patrones interesantes. Aquí mostramos los más comunes y cómo se forman.Sucesiones numéricas o aritméticas
Sucesiones especiales
Números triangulares o gráficas
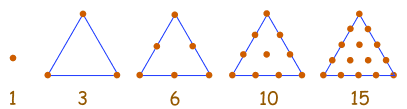
| 1, 3, 6, 10, 15, 21, 28, 36, 45, ... |
Esta sucesión se genera con un patrón de puntos que forma un triángulo.
Añadiendo otra fila de puntos y contando el total se encuentra el siguiente número de la sucesión.
Añadiendo otra fila de puntos y contando el total se encuentra el siguiente número de la sucesión.
Números cuadrados
| 1, 4, 9, 16, 25, 36, 49, 64, 81, ... |
El siguiente número se hace elevando su posición al cuadrado.
El segundo número es 2 al cuadrado (22 o 2×2)
El séptimo número es 7 al cuadrado (72 o 7×7) etc.
El segundo número es 2 al cuadrado (22 o 2×2)
El séptimo número es 7 al cuadrado (72 o 7×7) etc.
Números cúbicos
| 1, 8, 27, 64, 125, 216, 343, 512, 729, ... |
El siguiente número se calcula elevando su posición al cubo.
El segundo número es 2 al cubo (23 o 2×2×2)
El séptimo número es 7 al cubo (73 o 7×7×7) etc.
El segundo número es 2 al cubo (23 o 2×2×2)
El séptimo número es 7 al cubo (73 o 7×7×7) etc.
Números de Fibonacci(Serie Fibonacci)
| 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... |
El siguiente número se halla sumando los dos números delante de él.
El 2 se calcula sumando los dos números delante de él (1+1)
El 21 se calcula sumando los dos números delante de él (8+13)
El siguiente número de la sucesión sería 55 (21+34)
El 2 se calcula sumando los dos números delante de él (1+1)
El 21 se calcula sumando los dos números delante de él (8+13)
El siguiente número de la sucesión sería 55 (21+34)
El triángulo de Pascal
Una de las pautas de números más interesantes el es triángulo de Pascal (llamado así en honor de Blaise Pascal, un famoso matemático y filósofo francés).
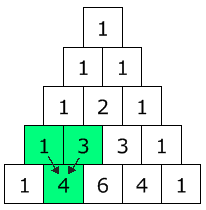
Para construir el triángulo, empieza con "1" arriba, y pon números debajo formando un triángulo.
(Aquí está remarcado que 1+3 = 4)
|  |
| Pautas en el triángulo |
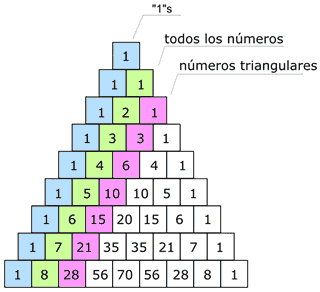 | Diagonales
La primera diagonal es, claro, sólo "unos", y la siguiente son todos los númerosconsecutivamente (1,2,3, etc.)
La tercera diagonal son los números triangulares
(La cuarta diagonal, que no hemos remarcado, son los números tetraédricos.)
| |||
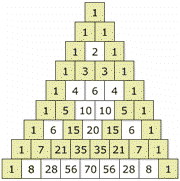
Pares e impares
Si usas distintos colores para los números pares e impares, obtienes un patrón igual al del Triángulo de Sierpinski
|  | |||
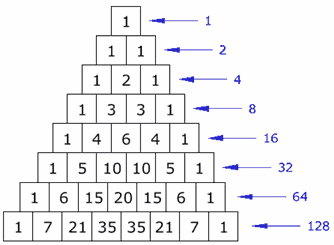 | Sumas horizontales
Se dobla cada vez (son las potencias de 2).
| |||
| ||||
| ||||
Otras sucesiones
¡Hay muchas más! Incluso se te pueden ocurrir a ti ...
Material obtenido de:
http://www.disfrutalasmatematicas.com/numeros-patrones.html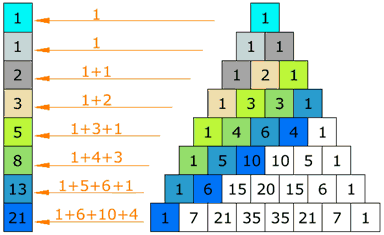

La pagina Khan Academy es una herramienta muy útil y muy divertida, ojala así fuera en todas las clases :)
ResponderEliminarPides mucho y das poco............el conocimiento es interesante, solo que no tienes interés.......
EliminarBuena manera de manejar las tecnoligias con la educacion
ResponderEliminarPersonalmente me pareció de mucha utilidad y muy interactiva la página web "Khan Academy", por lo que sería muy útil para estudiantes de todas las edades
ResponderEliminares una buena manera de aprender ya que se facilita
ResponderEliminarHola Luis
EliminarMe agrada que te sea útil el material...
Saludos
Excelente material maestra, gracias por compartirlo
ResponderEliminarHola maestra ¿tendrá las ECAS(secuencias didácticas?
ResponderEliminarClaro puedo compartirle mis planeaciones si me envía un mail a curienovak@gmail.com. En qué plantel se encuentra?
EliminarSaludos
Hola, que bien explicado, a mi también me interesan las ECAS, las puede compartir?
ResponderEliminarDisculpe, y las sucesiones simbólicas ¿cuáles son?
ResponderEliminarMuy buena guía e información para estudiar estos temas. Me preparo bien para mi clase de Mate Aplicada. Gracias!!
ResponderEliminar